En este breve escrito me propongo explicar como se obtienen las fórmulas para calcular el área del cuadrado, el rectángulo y el triángulo, haciendo uso de las nociones geométricas mas elementales; también se pondrá de manifiesto como escribir en lenjuage algebraico algunos de los conceptos geométricos. Como una herramiento poco justificada, se utilizará el hecho de que: dadas dos fracciones que tengan el mismo denominador, para hallar el numerador de su suma, basta con sumar unicamente sus numeradores y, para hallar el denominador de dicha suma, no hay que hacer más que tomar el mismo denominador.
Así pues, dada una figura plana, como puede ser un rectángulo, calcular su área consiste en asignarle un valor numérico a lo que podriamos llamar la superficie que dicha figura ocupa; para ello es necesario definir una unidad de medida, se acostumbra a utilizar la unidad cuadrada: por ejemplo el metro cuadrado o el centímetro cuadrado. Dicha unidad cuadrada se sefine como el espacio que ocupa un cuadrado cuyo lado mide exactamente una unidad de longitud:
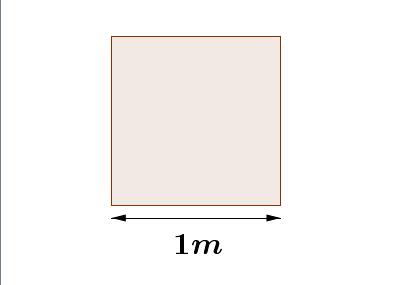
Área de un cuadrado
Así, por ejemplo, para calcular el área de un cuadrado cuyo lado mide tres unidades de longitud, debemos ser capaces de determinar cuantos cuadrados de longitud uno caben en dicho cuadrado: en otras palabras cuantas unidades de superficie equivalen a la superficie que ocupa un cuadrado cuyo lado mide tres unidades de longitud.
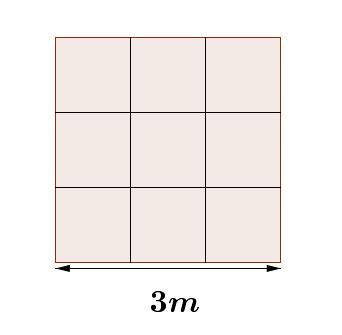
Como muestra la ilustración anterior, una vez trazada la cuadricula sobre nuestra figura plana, podemos contar el numero de cuadritos de longitud uno que equivalen a la figura; una vez hecho tal procedimiento habremos calculado el área de dicha figura.
Una forma más eficaz de contar los cuadrados consiste en agruparlos en ciertos grupos que tengan igual número de cuadrados; por ejemplo en columnas de tres cuadrados cada una; si hacemos eso, encontramos que se tienen tres grupos de tres cuadrados cada grupo; entonces el total se puede encontrar considerando tres veces cada a uno de estos grupos, teniendo así un total de nueve cuadraditos de lado uno; es decir: el área del cuadrado de lado tres es de nueve unidades cuadradas.
De aquí que una forma sencilla de calcular el área de un cuadrado consista en multiplicar por sí misma la longitud de su lado; es decir
donde 
representa la longitu de dicho lado.
Área de un rectángulo
El mismo procedimiento podemos aplicar para conocer cuál es el área de un rectángulo cuya base es de cinco unidades de longitud y cuya altura es de cuatro unidades de longitud.
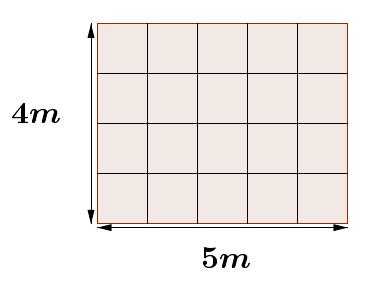
Trazamos la cuadricula y nuevamente agrupamos en columnas, se observa que cada grupo tiene cuatro unidades de área, y en total se forman cinco columnas. Entonces se tienen cinco columnas con cuatro cuadrados en cada columna; es decir se tienen cinco veces cuatro:
de aquí que lo fórmula para calcular el área del rectángulo es:
donde "b" es la base y "h" la altura.
Área de un triángulo
Presentemos ahora el problema de encontrar el área de un triángulo. Para resolverlo usaremos lo que ya se ha visto en los apartados anteriores; es decir de algún modo hay que utilizar las dos fórmulas anteriores. Para ello encerremos el triángulo en un rectángulo que tenga la misma base, como en la siguiente figura:
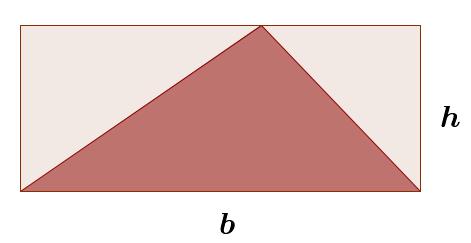
Si ahora colocamos el lápiz justo en la esquina superir del triangulo y trazamos una recta paralela a la altura del rectángulo, habremos partido a dicho rectángulo en dos rectangulos más pequeños y, simultaneamente habremos dividido el triangulo en dos triángulos más pequeños.
Observa además que el área que andamos buscando es exactamente la suma de las áreas de estos dos triángulos más pequeños y, a su vez, el área de cada uno de estos triángulos es la mitad del área del rectángulo que lo contiene.
Pero ya sabemos que el área de un rectángulo se obtine multiplicando su base por su altura. Entonces el área del triangulo que se quedá contenido es exactamente la mitad. Eso sería para cada uno de los triángulos en que dividimos al triángulo más grande (no olvidemos que nuestro objetivo es precisamente determinar el área de este triángulo más grande).
Ahora bien, si pudieramos medir cada uno de estos rectángulos, entonces el área total debe de estar dada por la suma:
Luego, como se trata de dos fracciones con el mismo denominador, basta sumar los denominadores, con lo que se tine que el área viene dada por
Ahora observemos que el numerador de esta fracción puede expresarse como: 
veces "h" más 
veces "h"; es decir, se tiene un total de 
veces "h", lo cual se representa por: 
. Así, se tiene que:
Finalmente, observa que 
(la suma de las bases de los triángolos pequeños es igual a la base del triángulo grande); en consecuencia, concluimos que, para culaquier triángulo de base "b" y altura "h" su área viene dada por la fórmula:
